The package mtdesign provides implementations of both
Simon (1989) and Mander & Thompson (2010). Other implementations of
Simon’s methods are available - for example, the ph2simon
function in the clinfun package (Seshan 2018), but these do
not provide easy access to non-optimal solutions in the way that
mtdesign does. I am not aware of any other R-based
implementations of Mander & Thompson’s extension to Simon.
Once available on CRAN, you can install mtdesign in the
usual way:
install.packages("mtdesign")
You can install the development version of mtdesign from
GitHub with:
devtools::install_github("openpharma/mtdesign")
# By policy, on CRAN, use only two cores, no matter how many are available.
if (requireNamespace("parallel", quietly = TRUE)) {
maxCores <- parallel::detectCores()
maxCores <- ifelse(identical(Sys.getenv("NOT_CRAN"), "true"), maxCores, min(maxCores, 2))
} else {
maxCores <- 1
}Suppose that treatments with a response rate of less than 5% are of no interest but those with a response rate of at least 25% are worthy of further development. A Simon’s 2-stage design to seek an efficacy signal with a significance level of 5% and a power of 80% is required.
library(mtdesign)
library(knitr)
library(dplyr)
#>
#> Attaching package: 'dplyr'
#> The following objects are masked from 'package:stats':
#>
#> filter, lag
#> The following objects are masked from 'package:base':
#>
#> intersect, setdiff, setequal, union
simonDesign <- obtainDesign(p0 = 0.05, p1 = 0.25, alpha = 0.05, beta = 0.2, mander = FALSE, parallel = FALSE)
simonDesign %>%
select(-Alpha, -Beta, -p0, -p1, -PETAlt, -AveSizeAlt) %>%
kable(digits = c(0, 0, 0, 0, 3, 3, 2, 1, NA))| nTotal | nStage1 | rTotal | rFutility | Type1 | Type2 | PETNull | AveSizeNull | Criterion |
|---|---|---|---|---|---|---|---|---|
| 17 | 9 | 2 | 0 | 0.047 | 0.188 | 0.63 | 12.0 | optimal |
| 16 | 12 | 2 | 0 | 0.043 | 0.199 | 0.54 | 13.8 | minimax |
The table shows that the optimal design for these requirements is 0/9 2/17. The expected sample size is 12.0 and the probability of early termination is 63%. The significance level actually achieved is 4.7% and the power level achieved is 100% - 18.8% = 81.2%.
The power curves for both designs are easily plotted.
powerPlot(simonDesign)
Obtaining the equivalent Mander & Thompson designs requires only a small change to the calls.
manderDesign <- obtainDesign(
p0 = 0.05,
p1 = 0.25,
alpha = 0.05,
beta = 0.2,
cores = maxCores
)
manderDesign %>%
select(-Alpha, -Beta, -p0, -p1) %>%
kable(digits = c(0, 0, 0, 0, 3, 3, 2, 2, 2, 1, NA))| nTotal | nStage1 | rTotal | rFutility | rSuccess | Type1 | Type2 | PETNull | PETAlt | AveSizeNull | AveSizeAlt | Criterion |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 17 | 9 | 2 | 0 | 2 | 0.047 | 0.19 | 0.64 | 0.47 | 11.9 | NA | optimalNull |
| 16 | 12 | 2 | 0 | 2 | 0.043 | 0.20 | 0.56 | 0.64 | 13.8 | NA | minimaxNull |
| 17 | 9 | 2 | 0 | 2 | 0.047 | 0.19 | 0.64 | 0.47 | 11.9 | NA | optimalAlt |
| 16 | 12 | 2 | 0 | 2 | 0.043 | 0.20 | 0.56 | 0.64 | 13.8 | NA | minimaxAlt |
powerPlot(manderDesign)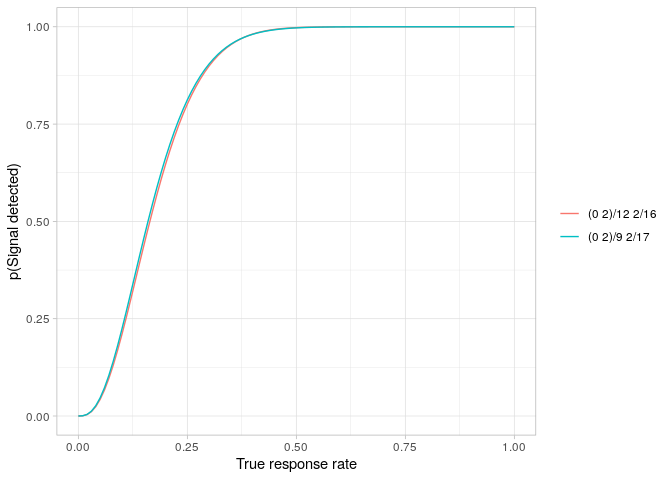
Suppose a trial, for whatever reason, is restricted to using 8 participants in each stage. As shown above, the optimal Simon’s two stage design is 0/9 2/17. That’s close to n1 = 8, n = 16. Is there a (slightly) sub-optimal design that has n1 = 8, n = 16?
x <- createGrid(p0 = 0.05, p1 = 0.25, alpha = 0.05, beta = 0.2, mander = FALSE)
y <- x %>% filter(nStage1 == 8, nTotal == 16)
z <- y %>% obtainDesign(cores = maxCores)
#> Warning: No acceptable designs were found.
if (nrow(z) == 0) {
print("No acceptable designs were found.")
} else {
select(-Alpha, -Beta, -p0, -p1, -PETAlt, -AveSizeAlt) %>%
z() %>%
select(-Alpha, -Beta, -p0, -p1, -PETAlt, -AveSizeAlt) %>%
kable(digits = c(0, 0, 0, 0, 3, 3, 2, 1, NA))
}
#> [1] "No acceptable designs were found."No, there isn’t. How close can we get?
z1 <- y %>% augmentGrid()
bestSize <- z1 %>%
filter(Type1 < Alpha) %>%
slice_min(Type2)
bestSize %>%
select(-Alpha, -Beta, -p0, -p1, -PETAlt, -AveSizeAlt) %>%
kable(
caption = "Best sub-optimal design with required significance level",
digits = c(0, 0, 0, 0, 3, 3, 2, 1, NA)
)| nTotal | nStage1 | rTotal | rFutility | Type1 | Type2 | PETNull | AveSizeNull |
|---|---|---|---|---|---|---|---|
| 16 | 8 | 2 | 0 | 0.039 | 0.229 | 0.66 | 10.7 |
Best sub-optimal design with required significance level
bestPower <- z1 %>%
filter(Type2 < Beta) %>%
slice_min(Type1)
bestPower %>%
select(-Alpha, -Beta, -p0, -p1, -PETAlt, -AveSizeAlt) %>%
kable(
caption = "Best sub-optimal design with required power",
digits = c(0, 0, 0, 0, 3, 3, 2, 1, NA)
)| nTotal | nStage1 | rTotal | rFutility | Type1 | Type2 | PETNull | AveSizeNull |
|---|---|---|---|---|---|---|---|
| 16 | 8 | 1 | 0 | 0.151 | 0.127 | 0.66 | 10.7 |
Best sub-optimal design with required power
So the choice lies between a design which achieves the required significance level but has a power of only 77.1% or one which has the required power but which has a significance level of 15.1%. Both designs accept the null hypothesis when no responders are seen in the first group of eight participants. They differ in the critical value at the end of stage 2: 1 to maintain the power, 2 to maintain the significance level.
The power curve for each of these designs can be compared with that for the globally optimal design.
plotData1 <- simonDesign %>%
filter(Criterion == "optimal") %>%
bind_rows(list(bestSize, bestPower))
powerPlot(plotData1)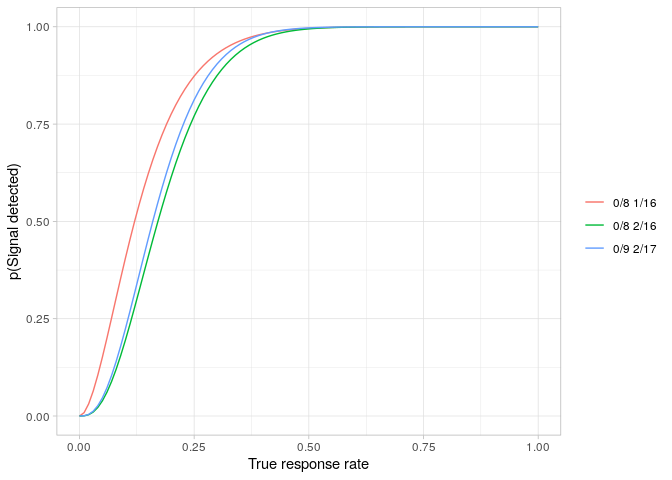
The mtdesign package consists of three main
functions:
createGrid creates the grid (of nStage1, rFutility,
nTotal and rTotal for Simon’s design or nStage1, rFutility, rSuccess,
nTotal and rTotal for a Mander & Thompson design) over which the
brute force search for the required design(s) is conductedaugmentGridtakes a grid created by
createGrid and adds columns for probability of early
termination, Type 1 error, Type 2 error and expected sample size to
it.obtainDesign takes an augmented grid and identifies the
optimal and minimax designsThe mtdesign package supports logging via the
futile.logger package (Rowe 2016). Most functions simply
report Entry and Exit at the DEBUG level.
The augmentGrid function reports steps of the
parallelisation process at the TRACE level.
There is no known closed form solution to obtaining solutions to
either Simon’s original equations nor Mander & Thompson’s
extensions. The mtdesign package uses a brute force
approach to evaluate the operating characteristics of all reasonable
potential designs. The grids can be quickly become large, particularly
for Mander & Thompson designs. For example,
createGrid(0.2, 0.4, alpha=0.1, beta=0.1) creates a grid of
almost 11 million candidate designs. mtdesign uses
paralellisation to attempt to speed up the evaluation of candidate
designs.
The augmentGrid function allows users some control over
the parallelisation process:
parallel parameter defaults to TRUE
and defines whether or not paralellisation is to be used.cores parameter specifies how many cores are to be
used. The default value, NA tells mtdesign to
use all available (as defined by parallel::detectCores()),
cores.minChunkSize determines the smallest grid of
candidate designs that will trigger paralellisation. The default value
is 100000.The parallel package is required for parallelisation. If
parallelisation is both needed (ie the grid size exceeds
minChunkSize) and requested but the parallel
package has not been installed, an error message is thrown and
augmentation of the grid stops. If paralellisation is not requested and
the grid contains one million or more rows, a warning is produced.
If, when installing or using the mtdesign package, you
get an error regarding a syntax error in an.hpp file,
similar to the following
.../BH/include/boost/math/tools/fraction.hpp:84:48: error: ‘long double’ is not a class, struct, or union type using value_type = typename T::value_type;the issue is most likely a mismatch between the g++ compiler being
used and the headers supplied by the BH package. There are
only two solutions that I know of:
BH package you are using.
The appropriate package version depends on the version of the g++
compiler you are using.